문제1 - 큰 수의 법칙 (Law of Large Numbers)

상황 설명

-큰 수의 법칙 (Law of Large Numbers)

LLN

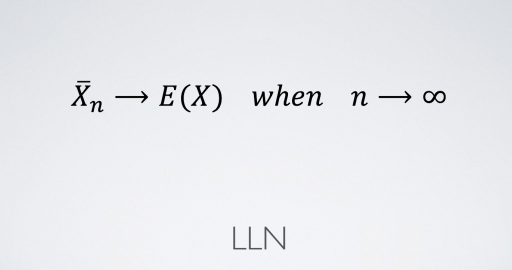
LLN으로 줄여 말하는 큰수의 법칙을 구글에 검색해보면

우연한 사건이나 특정 결과의 발생을 정확히 예측하기란 거의 불가능하지만 반복 시행하는 횟수가 많거나 표본이 커질수록 일정한 수준으로 수렴하게 되고 비교적 정확한 예측이 가능하다는 의미

라고 찾을 수 있다.

 

확률

 

간단한 예를 들어보면, 동전을 던져 앞면이 나올 확률을 구해보자.

10번 시행시 7번이 앞면이 나온다면, 확률은 70% 이다.

100번 시행시 52번 앞면이 나온다면, 확률은 52% 이고,

1000번 시행시 502번 앞면이 나온다면, 확률은 50.2%이다.

 

시행 횟수가 많아질 수록 우리가 생각하는 답인 50%에 근접함을 볼 수 있다.

 

정규 분포표

 

다음은 정규분포표를 나타낸다.

randn() 함수는 평균 0, 표준편차 1의 정규분포 확률을 통해 난수를 만든다.

즉, randn() 함수에서 -1 과 1 사이의 값이 나올 확률이 68.2% 라는 것이다.

 

문제

문제 1: randn() 함수가 정규분포를 따르는지 확인하고자 한다.

-1 과 1 사이의 값이 나올 확률이 68.2%인지 파이썬을 통해 확인해보자.

 

힌트 1:

힌트 1

 

for i in randn():

    #...

 

힌트 2:

import numpy as np
from numpy.random import randn

N = _
counter = _

for __ randn(N):
	if(___ and ___):
    	counter = ___
answer = counter / N

print(answer)

빈칸을 생각해보자.

 

정답은 다음 글에 쓰도록 하겠다.